Astronomy in medieval Islam

In the history of astronomy, Islamic astronomy or Arabic astronomy refers to the astronomical developments made in the Islamic world, particularly during the Islamic Golden Age (8th-15th centuries),^[1] and mostly written in the Arabic language. These developments mostly took place in the Middle East, Central Asia, Al-Andalus, and North Africa, and later in the Far East and India. It closely parallels the genesis of other Islamic sciences in its assimilation of foreign material and the amalgamation of the disparate elements of that material to create a science with Islamic characteristics. These included Sassanid, Hellenistic and Indian works in particular, which were translated and built upon.^[2] In turn, Islamic astronomy later had a significant influence on Indian,^[3] Byzantine^[4] and European^[5] astronomy (see Latin translations of the 12th century) as well as Chinese astronomy^[6] and Malian astronomy.^[7][8]

A significant number of stars in the sky, such as Aldebaran and Altair, and astronomical terms such as alhidade, azimuth, and almucantar, are still referred to by their Arabic names.^[9] A large corpus of literature from Islamic astronomy remains today, numbering approximately 10,000 manuscripts scattered throughout the world, many of which have not been read or catalogued. Even so, a reasonably accurate picture of Islamic activity in the field of astronomy can be reconstructed.^[10]

Islam and astronomy

Islam has affected astronomy directly and indirectly. A major impetus for the flowering of astronomy in Islam came from religious observances, which presented an assortment of problems in mathematical astronomy, specifically in spherical geometry.^[2]

Background

In the 7th century, both Christians and Jews observed holy days, such as Easter and Passover, whose timing was determined by the phases of the moon. Both communities had confronted the fact that the approximately 29.5-day lunar months are not commensurable with the 365-day solar year. To solve the problem, Christians and Jews had adopted a scheme based on a discovery made in circa 430 BC by the Athenian astronomer Meton. In the 19-year Metonic cycle, there were 12 years of 12 lunar months and seven years of 13 lunar months. The periodic insertion of a 13th month kept calendar dates in step with the seasons.^[2]

On the other hand, astronomers used Ptolemy's way to calculate the place of the moon and stars. The method Ptolemy used to solve spherical triangles was a clumsy one devised late in the 1st century by Menelaus of Alexandria. It involved setting up two intersecting right triangles; by applying Menelaus' theorem it was possible to solve one of the six sides, but only if the other five sides were known. To tell the time from the sun's altitude, for instance, repeated applications of Menelaus' theorem were required. For medieval Islamic astronomers, there was an obvious challenge to find a simpler trigonometric method.^[2]

Islamic attitude towards astronomy

Islam advised Muslims to find ways of using the stars. The Qur'an says: "And it is He who ordained the stars for you that you may be guided thereby in the darkness of the land and the sea."^[11] On the basis of this advice Muslims began to develop better observational and navigational instruments, thus most navigational stars today have Arabic names.^[2]

Other influences of the Qur'an on Islamic astronomy included its "insistence that the Universe is ruled by a single set of laws" which was "rooted in the Islamic concept of tawhîd, the unity of God", as well its "greater respect for empirical data than was common in the preceding Greek civilization" which inspired Muslims to place a greater emphasis on empirical observation,^[12] in contrast to ancient Greek philosophers such as the Platonists who expressed a general distrust towards the senses and instead viewed reason alone as being sufficient to understanding nature. The Qur'an's insistence on observation, reason and contemplation ("see", "think" and "contemplate"), on the other hand, led Muslims to develop an early scientific method based on these principles, particularly empirical observation. Muhammad Iqbal writes:^[13]

“The general empirical attitude of the Qur'an which engendered in its followers a feeling of reverence for the actual, and ultimately made them the founders of modern science. It was a great point to awaken the empirical spirit in an age that renounced the visible as of no value in men's search after God.”

Several hadiths attributed to Muhammad also show that he was generally opposed to astrology as well as superstition in general. An example of this is when an eclipse occurred during his son Ibrahim ibn Muhammad's death, and rumours began spreading about this being God's personal condolence. Muhammad is said to have replied:^[14]

"An eclipse is a phenomenon of nature & has no relation to the death or birth of a human being."

From the 12th century onwards, Islamic astronomy began becoming a science primarily dependant upon observation rather than philosophy, primarily due to religious opposition from Islamic theologians of the Ash'ari school, most prominently Al-Ghazali, who opposed the interference of Aristotelian physics and Aristotelian cosmology in astronomy, opening up possibilities for an astronomy unrestrained by Aristotelian philosophy.^[15][16] For example, the Ash'ari doctrine influenced the theologian Fakhr al-Din al-Razi (1149–1209) to reject the Aristotelian notion of the Earth's centrality within the universe and instead propose the notion of a multiverse consisting of countless worlds and universes, "such that each one of those worlds be bigger and more massive than this world as well as having the like of what this world has." Al-Razi also criticized the Aristotelian notion of solid celestial spheres and suggested these may be "merely the abstract orbit traced by the stars."^[17] Later in the century, the Islamic theologian Adud al-Din al-Iji (1281–1355), under the influence of the Ash'ari doctrine of occasionalism, which maintained that all physical effects were caused directly by God's will, rejected the Aristotelian principle of an innate principle of circular motion in the heavenly bodies,^[18] and maintained that the celestial spheres were "imaginary things" and "more tenuous than a spider's web".^[16] Under such influences, Ali al-Qushji (d. 1474) rejected Aristotelian physics and completely separated it from astronomy, allowing astronomy to become a purely empirical and mathematical science. This allowed him to explore alternatives to the Aristotelian notion of a stationery Earth, as he explored the idea of a moving Earth. He concluded, on the basis of empirical evidence rather than speculative philosophy, that the moving Earth theory is just as likely to be true as the stationary Earth theory and that it is not possible to empirically deduce which theory is true (see Astronomical physics and Earth's motion section below).^[15][16]

Islamic rules

Arabic manuscript illumination from the twelfth century CE showing various historical figures and scholars in medieval Islam

There are several rules in Islam which lead Muslims to use better astronomical calculations and observations.

The first issue is the Islamic calendar. The Qur'an says: "The number of months in the sight of Allah is twelve (in a year) so ordained by Him the day He created the heavens and the earth; of them four are sacred; that is the straight usage."^[2][19] Therefore Muslims could not follow the Christian or Hebrew calendars and they thus had to develop a new one.

The other issue is moon sighting. Islamic months do not begin at the astronomical new moon, defined as the time when the moon has the same celestial longitude as the sun and is therefore invisible; instead they begin when the thin crescent moon is first sighted in the western evening sky.^[2] The Qur'an says: "They ask you about the waxing and waning phases of the crescent moons, say they are to mark fixed times for mankind and Hajj."^[20][21] This led Muslims to find the phases of the moon in the sky, and their efforts led to new mathematical calculations and observational instruments, as well as a special science being formed specifically for moon sighting.^[22]

Muslims are also expected to pray towards the Kaaba in Mecca and orient their mosques in that direction. Thus they need to determine the direction of Mecca from a given location.^[23][24] Another influencing factor is the time of Salah. Muslims need to determine from celestial bodies the proper times for the prayers at sunrise, at midday, in the afternoon, at sunset, and in the evening.^[2][25]

Necessity of spherical geometry

An illustration from al-Biruni's Persian book. It shows different phases of the moon.

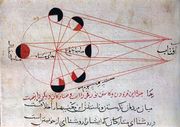
Predicting just when the crescent moon would become visible is a special challenge to Islamic mathematical astronomers. Although Ptolemy's theory of the complex lunar motion was tolerably accurate near the time of the new moon, it specified the moon's path only with respect to the ecliptic. To predict the first visibility of the moon, it was necessary to describe its motion with respect to the horizon, and this problem demands a more sophisticated spherical geometry.^[26] Finding the direction of Mecca and the time of Salah are the reasons which led to Muslims making advances in spherical geometry. Solving any of these problems involves finding the unknown sides or angles of a triangle on the celestial sphere from the known sides and angles. A way of finding the time of day, for example, is to construct a triangle whose vertices are the zenith, the north celestial pole, and the sun's position. The observer must know the altitude of the sun and that of the pole; the former can be observed, and the latter is equal to the observer's latitude. The time is then given by the angle at the intersection of the meridian (the arc through the zenith and the pole) and the sun's hour circle (the arc through the sun and the pole).^[2][25]

History

Pre-Islamic Arabian knowledge of stars was empirical; their knowledge was what they observed regarding the rising and setting of stars. The rise of Islam is claimed to have provoked increased Arab thought in this field.^[27] The foundations of Islamic astronomy closely parallel the genesis of other Islamic sciences in its assimilation of foreign material and the amalgamation of the disparate elements of that material to create a science that was essentially Islamic. These include Indian, Sassanid and Hellenistic works which were translated and built upon.

The science historian Donald Routledge Hill has divided the history of Islamic astronomy into the four following distinct time periods in its history:^[27]

• Assimilation and syncretization of earlier Hellenistic, Indian and Sassanid astronomy (700—825 AD)
• Vigorous investigation, and acceptance and modification to the Ptolemaic system (825—1025 AD)
• Flourishing of a distinctive Islamic system of astronomy (1025—1450 AD)
• Stagnation, where few significant contributions were made (1450—1900 AD)

610-700

From the beginning, Muslim community in Medina sight new moon to determine the lunar months especially Ramadan and holy days.

In approximately 638 A.D, Caliph Umar introduced a new lunar calendar based on the Islamic viewpoint. This calendar has twelve lunar months, the beginnings of which are determined by the sighting of the crescent moon. This calendar is about 11 days shorter than the solar year. This calendar is still in use for religious purposes among Muslims.^[2][28]

700-825

This period was most notably the period of assimilation and syncretization of earlier Hellenistic, Indian and Sassanid astronomy occurred during the 8th and early 9th centuries.

Impetus

Historians point out several factors that fostered the growth of Islamic astronomy. The first was the proximity of the Muslim world to the world of ancient learning. Much of the ancient Greek, Sanskrit and Middle Persian texts were translated into Arabic during the 9th century. This process was enhanced by the tolerance towards scholars of other religions.^[2]

Another impetus came from Islamic religious observances, which presented a host of problems in mathematical astronomy. In solving these religious problems the Islamic scholars went far beyond the Greek mathematical methods.^[2]

Ancient influences and translation movement

During this period, a number of Sanskrit and Middle Persian texts were first translated into Arabic. The most notable of the texts was Zij al-Sindhind,^[29] based on the Surya Siddhanta and the works of Brahmagupta, and translated by Muhammad al-Fazari and Yaqūb ibn Tāriq in 777. Sources indicate that the text was translated after an Indian astronomer visited the court of Caliph Al-Mansur in 770. The most notable Middle Persian text translated was the Zij al-Shah, a collection of astronomical tables compiled in Sassanid Persia over two centuries.

Fragments of text during this period indicate that Arabs adopted the sine function (inherited from Indian trigonometry) instead of the chords of arc used in Hellenistic mathematics.^[27] Another Indian influence was an approximate formula used for timekeeping by Muslim astronomers.^[30]

A page from Ptolemy's Almagest.

Islamic interest in astronomy ran parallel to the interest in mathematics. Especially noteworthy in this regard was the Almagest (c. 150) of the astronomer Ptolemy (c. 100-178). The Almagest was a landmark work in its field, assembling, as Euclid's Elements had previously done with geometrical works, all extant knowledge in the field of astronomy that was known to the author. This work was originally known as The Mathematical Composition, but after it had come to be used as a text in astronomy, it was called The Great Astronomer. The Islamic world called it The Greatest prefixing the Greek work megiste (greatest) with the article al- and it has since been known to the world as Al-megiste or, after popular use in Western translation, Almagest.^[31] though much of the Almagest was incorrect, even in premise, it remained a standard astronomical text in both the Islamic world and Europe until the Maragha Revolution and Copernican Revolution.^[32] Ptolemy also produced other works, such as Optics, Harmonica, and some suggest he also wrote Tetrabiblon.

The Almagest was a particularly unifying work for its exhaustive lists of astronomical phenomena. He drew up a list of chronological tables of Assyrian, Persian, Greek, and Roman kings for use in reckoning the lapse of time between known astronomical events and fixed dates. In addition to its relevance to calculating accurate calendars, it linked far and foreign cultures together by a common interest in the stars and astrology. The work of Ptolemy was replicated and refined over the years under Arab, Persian and other Muslim astronomers and astrologers.

825-1025

The period throughout the 9th, 10th and early 11th centuries was one of vigorous investigation, in which the superiority of the Ptolemaic system of astronomy was accepted and significant contributions made to it. Astronomical research was greatly supported by the Abbasid caliph al-Mamun. Baghdad and Damascus became the centers of such activity. The caliphs not only supported this work financially, but endowed the work with formal prestige.^[33]

Early observational astronomy

Al-Khwarizmi, the father of algebra and algorithms and a Persian Astronomer, wrote the Zij al-Sindh, the first original Zij in Islamic astronomy.

In observational astronomy, the first major original Muslim work of astronomy was Zij al-Sindh by al-Khwarizimi in 830. The work contains tables for the movements of the sun, the moon and the five planets known at the time. The work is significant as it introduced Indian and Ptolemaic concepts into Islamic sciences. This work also marked the turning point in Islamic astronomy. Hitherto, Muslim astronomers had adopted a primarily research approach to the field, translating works of others and learning already discovered knowledge. Al-Khwarizmi's work marked the beginning of non-traditional methods of study and calculations.^[34]

Between 825 to 835, Habash al-Hasib al-Marwazi conducted various observations at the Al-Shammisiyyah observatory in Baghdad, where he estimated a number of geographic and astronomical values.^[35] He compiled his results in The Book of Bodies and Distances, in which many of his estimates come closer to modern values than any of his predecessors. For example, he estimated the Moon's diameter as 3,037 km (equivalent to 1,519 km radius) and its distance from the Earth as 215,209 miles, which come close to the currently accepted values of 1,735 km radius and 238,857 miles distance, respectively.^[36]

In 850, al-Farghani wrote Kitab fi Jawani ("A compendium of the science of stars"). The book primarily gave a summary of Ptolemic cosmography. However, it also corrected Ptolemy's Almagest based on findings of earlier Iranian astronomers. Al-Farghani gave revised values for the obliquity of the ecliptic, the precessional movement of the apogees of the sun and the moon, and the circumference of the earth. The books were widely circulated through the Muslim world, and even translated into Latin.^[37]

Muhammad ibn Jābir al-Harrānī al-Battānī (Albatenius) (853-929) produced "improved tables of the orbits of the sun and the moon" that "contained his great discovery that the direction of the sun's excentric ... , as recorded by Ptolemy, was changing."^[38] Among other things, he worked on timing the first appearance of the moon's crescent following a new moon, the lengths of the solar and sidereal years, the prediction of eclipses, and the phenomenon of parallax.^[39] Around the same time, Yahya Ibn Abi Mansour carried out extensive observations and tests, and wrote the Al-Zij al-Mumtahan, in which he completely revised the Almagest values.^[40]

Azophi's Book of Fixed Stars, which described more than a thousand stars in detail and gave the first descriptions on the Andromeda Galaxy and Large Magellanic Cloud. The constellation pictured here is Sagittarius.

In the 10th century, Abd al-Rahman al-Sufi (Azophi) carried out observations on the stars and described their positions, magnitudes, brightness, and colour and drawings for each constellation in his Book of Fixed Stars (964). He also gave the first descriptions and pictures of "A Little Cloud" now known as the Andromeda Galaxy. He mentions it as lying before the mouth of a Big Fish, an Arabic constellation. This "cloud" was apparently commonly known to the Isfahan astronomers, very probably before 905 AD.^[41] The first recorded mention of the Large Magellanic Cloud was also given by Abd Al-Rahman al-Sufi.^[42][43]

Ibn Yunus observed more than 10,000 entries for the sun's position for many years using a large astrolabe with a diameter of nearly 1.4 meters. His observations on eclipses were still used centuries later in Simon Newcomb's investigations on the motion of the moon, while his other observations inspired Laplace's Obliquity of the Ecliptic and Inequalities of Jupiter and Saturn. ^[44] Abu-Mahmud al-Khujandi relatively accurately computed the axial tilt to be 23°32'19" (23.53°).^[45]

In 1006, the Egyptian astronomer Ali ibn Ridwan observed SN 1006, the brightest supernova in recorded history, and left a detailed description of the temporary star. He says that the object was two to three times as large as the disc of Venus and about one-quarter the brightness of the Moon, and that the star was low on the southern horizon. Monks at the Benedictine abbey at St. Gall later corroborated bin Ridwan's observations as to magnitude and location in the sky.

Rejection of Heliocentrism

Due to the scientific dominance of the Ptolemaic system in Islamic astronomy, the Muslim astronomers accepted unanimously the geocentric model.^[46] However, several Muslim scholars questioned the Earth's apparent immobility^[15][16] and centrality within the universe.^[17] Alhazen wrote a scathing critique of Ptolemy's model in his Doubts on Ptolemy (c. 1028), which some have interpreted to imply he was criticizing Ptolemy's geocentrism,^[47] but most agree that he was actually criticizing the details of Ptolemy's model rather than his geocentrism.^[48] Alhazen did, however, later propose the Earth's rotation on its axis in The Model of the Motions (c. 1038).^[49]

Abu Rayhan Biruni (b. 973) discussed the possibility of whether the Earth rotated about its own axis and around the Sun, but in his Masudic Canon, he set forth the principles that the Earth is at the center of the universe and that it has no motion of its own.^[50] He was aware that if the Earth rotated on its axis and around the Sun, this would be consistent with his astronomical parameters,^[51] but he considered this a philosophical problem rather than a mathematical one.^[5]

Universal cosmology

In contrast to ancient Greek philosophers who believed that the universe had an infinite past with no beginning, medieval philosophers and theologians developed the concept of the universe having a finite past with a beginning (see Temporal finitism). This view was inspired by the creation myth shared by the three Abrahamic religions: Judaism, Christianity and Islam. The Christian philosopher, John Philoponus, presented the first such argument against the ancient Greek notion of an infinite past. His arguments were adopted by many most notably; early Muslim philosopher, Al-Kindi (Alkindus); the Jewish philosopher, Saadia Gaon (Saadia ben Joseph); and the Muslim theologian, Al-Ghazali (Algazel). They used two logical arguments against an infinite past, the first being the "argument from the impossibility of the existence of an actual infinite", which states:^[52]

"An actual infinite cannot exist."

"An infinite temporal regress of events is an actual infinite."

"An infinite temporal regress of events cannot exist."

The second argument, the "argument from the impossibility of completing an actual infinite by successive addition", states:^[52]

"An actual infinite cannot be completed by successive addition."

"The temporal series of past events has been completed by successive addition."

"The temporal series of past events cannot be an actual infinite."

Both arguments were adopted by later Christian philosophers and theologians, and the second argument in particular became more famous after it was adopted by Immanuel Kant in his thesis of the first antimony concerning time.^[52]

Physical cosmology, kinematic astronomy,
and astronomical observations

Mustansiriya University in Baghdad (the minaret in the background was used for astronomical purposes)

In the 9th century, the eldest Banū Mūsā brother, Ja'far Muhammad ibn Mūsā ibn Shākir, made significant contributions to astrophysics and celestial mechanics. He was the first to hypothesize that the heavenly bodies and celestial spheres are subject to the same laws of physics as Earth, unlike the ancients who believed that the celestial spheres followed their own set of physical laws different from that of Earth.^[53] In the 10th century, Muhammad ibn Jābir al-Harrānī al-Battānī (Albatenius) (853-929) introduced the idea of testing "past observations by means of new ones".^[54] This led to the use of exacting empirical observations and experimental techniques by Muslim astronomers from the 11th century onwards.^[55]

In the early 11th century, Ibn al-Haytham (Alhazen) wrote the Maqala fi daw al-qamar (On the Light of the Moon) some time before 1021. This was the first attempt successful at combining mathematical astronomy with physics and the earliest attempt at applying the experimental method to astronomy and astrophysics. He disproved the universally held opinion that the moon reflects sunlight like a mirror and correctly concluded that it "emits light from those portions of its surface which the sun's light strikes." In order to prove that "light is emitted from every point of the moon's illuminated surface," he built an "ingenious experimental device." Ibn al-Haytham had "formulated a clear conception of the relationship between an ideal mathematical model and the complex of observable phenomena; in particular, he was the first to make a systematic use of the method of varying the experimental conditions in a constant and uniform manner, in an experiment showing that the intensity of the light-spot formed by the projection of the moonlight through two small apertures onto a screen diminishes constantly as one of the apertures is gradually blocked up."^[56]

Ibn al-Haytham, in his Book of Optics (1021), also maintained that the celestial spheres do not consist of solid matter, and that the heavens are less dense than the air. These views were later repeated by Witelo and had a significant influence on the Copernican and Tychonic systems of astronomy.^[57]

Ibn al-Haytham also refuted Aristotle's view on the Milky Way galaxy. Aristotle believed the Milky Way to be caused by "the ignition of the fiery exhalation of some stars which were large, numerous and close together" and that the "ignition takes place in the upper part of the atmosphere, in the region of the world which is continuous with the heavenly motions."^[58] Ibn al-Haytham refuted this by making the first attempt at observing and measuring the Milky Way's parallax,^[59] and he thus "determined that because the Milky Way had no parallax, it was very remote from the earth and did not belong to the atmosphere."^[60]

Also in the early 11th century, Abū Rayhān al-Bīrūnī introduced the experimental method into astronomy and was the first to conduct elaborate experiments related to astronomical phenomena.^[61] He discovered the Milky Way galaxy to be a collection of numerous nebulous stars.^[62] In Afghanistan, he observed and described the solar eclipse on April 8, 1019, and the lunar eclipse on September 17, 1019, in detail, and gave the exact latitudes of the stars during the lunar eclipse.^[61]

1025-1450

During this period, a distinctive Islamic system of astronomy flourished. It was Greek tradition to separate mathematical astronomy (as typified by Ptolemy) from philosophical cosmology (as typified by Aristotle). Muslim scholars developed a program of seeking a physically real configuration (hay'a) of the universe, that would be consistent with both mathematical and physical principles. Within the context of this hay'a tradition, Muslim astronomers began questioning technical details of the Ptolemaic system of astronomy.^[63] Most of these criticisms, however, continued to follow the Ptolemaic astronomical paradigm, remaining within the geocentric framework.^[64] As the historian of astronomy, A. I. Sabra, noted:

"All Islamic astronomers from Thabit ibn Qurra in the ninth century to Ibn al-Shatir in the fourteenth, and all natural philosophers from al-Kindi to Averroes and later, are known to have accepted what Kuhn has called the "two-sphere universe" ...—the Greek picture of the world as consisting of two spheres of which one, the celestial sphere made up of a special element called aether, concentrically envelops the other, where the four elements of earth, water, air, and fire reside."^[65]

Some Muslim astronomers, however, most notably Abū Rayhān al-Bīrūnī and Nasīr al-Dīn al-Tūsī, discussed whether the Earth moved and considered how this might be consistent with astronomical computations and physical systems.^[66] Several other Muslim astronomers, most notably those following the Maragha school of astronomy, developed non-Ptolemaic planetary models within a geocentric context that were later adapted by the Copernican model in a heliocentric context.

Refutations of astrology

The study of astrology was refuted by several Muslim writers, including al-Farabi, Ibn al-Haytham, Avicenna, Abu Rayhan al-Biruni and Averroes. Their reasons for refuting astrology were often due to both scientific (the methods used by astrologers being conjectural rather than empirical) and religious (conflicts with orthodox Islamic scholars) reasons.^[67]

Ibn Qayyim Al-Jawziyya (1292–1350), in his Miftah Dar al-SaCadah, used empirical arguments in astronomy in order to refute the practice of astrology and divination.^[68] He recognized that the stars are much larger than the planets, and that Mercury is the smallest planet known to them, and thus argued:^[69]

"And if you astrologers answer that it is precisely because of this distance and smallness that their influences are negligible, then why is it that you claim a great influence for the smallest heavenly body, Mercury? Why is it that you have given an influence to al-Ra's and al-Dhanab, which are two imaginary points [ascending and descending nodes]?"

Al-Jawziyya also recognized the Milky Way galaxy as "a myriad of tiny stars packed together in the sphere of the fixed stars" and thus argued that "it is certainly impossible to have knowledge of their influences."^[69]

Astrophysics and celestial mechanics

In astrophysics and celestial mechanics, Abū Rayhān al-Bīrūnī described the Earth's gravitation as:

"The attraction of all things towards the centre of the earth."

Al-Biruni also discovered that gravity exists within the heavenly bodies and celestial spheres, and he criticized the Aristotelian views of them not having any levity or gravity and of circular motion being an innate property of the heavenly bodies.^[70]

Also in the 12th century, Fakhr al-Din al-Razi participated in the debate among Islamic scholars over whether the celestial spheres or orbits (falak) are "to be considered as real, concrete physical bodies" or "merely the abstract circles in the heavens traced out year in and year out by the various stars and planets." He points out that many astronomers prefer to see them as solid spheres "on which the stars turn," while others, such as the Islamic scholar Dahhak, view the celestial sphere as "not a body but merely the abstract orbit traced by the stars." Al-Razi himself remains "undecided as to which celestial models, concrete or abstract, most conform with external reality," and notes that "there is no way to ascertain the characteristics of the heavens," whether by "observable" evidence or by authority (al-khabar) of "divine revelation or prophetic traditions." He concludes that "astronomical models, whatever their utility or lack thereof for ordering the heavens, are not founded on sound rational proofs, and so no intellectual commitment can be made to them insofar as description and explanation of celestial realities are concerned."^[17]

Beginning of hay'a program

Ibn al-Haytham (Alhacen) was a pioneer of the Muslim haya tradition of astronomy, presented the first critique and reform of Ptolemy's model, and introduced experimentation to astrophysics.

Between 1025 and 1028, Ibn al-Haytham (Latinized as Alhazen), began what has been called the hay'a tradition of Islamic astronomy with his Al-Shuku ala Batlamyus (Doubts on Ptolemy). The hay'a tradition was concerned with accommodating mathematical hypotheses within "a configuration (hay'a) of physical orbs and spheres each of which turning uniformly about its own axis," thereby producing "a physically plausible ... description of what actually took place in the heavens."^[71] While maintaining the physical reality of the geocentric model, he was the first to criticize Ptolemy's astronomical system, which he criticized on empirical, observational and experimental grounds,^[72] and for relating actual physical motions to imaginary mathematical points, lines and circles:

"Ptolemy assumed an arrangement that cannot exist, and the fact that this arrangement produces in his imagination the motions that belong to the planets does not free him from the error he committed in his assumed arrangement, for the existing motions of the planets cannot be the result of an arrangement that is impossible to exist."^[73]

Ibn al-Haytham developed a physical structure of the Ptolemaic system in his Treatise on the configuration of the World, or Maqâlah fî hay'at al-‛âlam, which became an influential work in the hay'a tradition.^[74] In his Epitome of Astronomy, he insisted that the heavenly bodies "were accountable to the laws of physics."^[75]

In 1038, Ibn al-Haytham described the first non-Ptolemaic configuration in The Model of the Motions. His reform was not concerned with cosmology, as he developed a systematic study of celestial kinematics that was completely geometric. This in turn led to innovative developments in infinitesimal geometry.^[76] His reformed model was the first to reject the equant^[77] and eccentrics,^[78] separate natural philosophy from astronomy, free celestial kinematics from cosmology, and reduce physical entities to geometrical entities. The model also propounded the Earth's rotation about its axis,^[79] and the centres of motion were geometrical points without any physical significance, like Johannes Kepler's model centuries later.^[80] Ibn al-Haytham also describes an early version of Occam's razor, where he employs only minimal hypotheses regarding the properties that characterize astronomical motions, as he attempts to eliminate from his planetary model the cosmological hypotheses that cannot be observed from Earth.^[81]

Al-Biruni was the first to conduct elaborate experiments related to astronomical phenomena, and he introduced the analysis of the acceleration of planets, discovered that the motions of the solar apogee and precession are not identical, discussed the possibility of heliocentrism, and suggested that the Earth's rotation on its axis would be consistent with his astronomical parameters.

Early alternative models

In 1030, Abū al-Rayhān al-Bīrūnī discussed the Indian planetary theories of Aryabhata, Brahmagupta and Varahamihira in his Ta'rikh al-Hind (Latinized as Indica). Biruni stated that Brahmagupta and others consider that the earth rotates on its axis and Biruni noted that this does not create any mathematical problems.^[82]

Abu Said al-Sijzi, a contemporary of al-Biruni, suggested the possible heliocentric movement of the Earth around the Sun, which al-Biruni did not reject.^[83] Al-Biruni agreed with the Earth's rotation about its own axis, and while he was initially neutral regarding the heliocentric and geocentric models,^[84] he considered heliocentrism to be a philosophical problem.^[5] He remarked that if the Earth rotates on its axis and moves around the Sun, it would remain consistent with his astronomical parameters:^[51]

"Rotation of the earth would in no way invalidate astronomical calculations, for all the astronomical data are as explicable in terms of the one theory as of the other. The problem is thus difficult of solution."

In 1031, al-Biruni completed his extensive astronomical encyclopaedia Kitab al-Qanun al-Mas'udi (Latinized as Canon Mas’udicus),^[85] in which he recorded his astronomical findings and formulated astronomical tables. In it he presented a geocentric model, tabulating the distance of all the celestial spheres from the central Earth, computed according to the principles of Ptolemy's Almagest.^[86] The book introduces the mathematical technique of analysing the acceleration of the planets, and first states that the motions of the solar apogee and the precession are not identical. Al-Biruni also discovered that the distance between the Earth and the Sun is larger than Ptolemy's estimate, on the basis that Ptolemy disregarded annular eclipses.

In 1070, Abu Ubayd al-Juzjani, a pupil of Avicenna, proposed a non-Ptolemaic configuration in his Tarik al-Aflak. In his work, he indicated the so-called "equant" problem of the Ptolemic model, and proposed a solution for the problem. He claimed that his teacher Avicenna had also worked out the equant problem.^[87]

Andalusian Revolt

Muladi art from Toledo in Al-Andalus depicting the Alcázar in the year 976.AD

Averroes rejected the eccentric deferents introduced by Ptolemy. He rejected the Ptolemaic model and instead argued for a strictly concentric model of the universe.

In the 11th-12th centuries, astronomers in al-Andalus such as Al-Majriti and Ibn al-Saffar introduced various works and used various instruments. Later Abu al-Salt is credited to have introduced the early astronomical works of Al-Andalus to North Africa where they have been preserved. Their students took up the challenge earlier posed by Ibn al-Haytham, namely to develop an alternate non-Ptolemaic configuration that evaded the errors found in the Ptolemaic model.^[88] Like Ibn al-Haytham's critique, the anonymous Andalusian work, al-Istidrak ala Batlamyus (Recapitulation regarding Ptolemy), included a list of objections to Ptolemic astronomy. This marked the beginning of the Andalusian school's revolt against Ptolemaic astronomy, sometimes called the "Andalusian Revolt".^[89]

In the 12th century, under the influence of Ibn Tufail, the philosopher, Averroes and the astronomer, al-Bitruji, rejected the epicycles and eccentrics introduced by Ptolemy. They considered the Ptolemaic model to be inconsistent with Aristotle's physical principles and argued for a strictly concentric model of the universe. Al-Bitruji failed in his attempt to make an accurate model of the motions of the planets employing homocentric spheres.^[90] Averroes wrote the following criticism of the Ptolemaic model of planetary motion:^[2]

"To assert the existence of an eccentric sphere or an epicyclic sphere is contrary to nature. [...] The astronomy of our time offers no truth, but only agrees with the calculations and not with what exists."

Averroes' contemporary, Maimonides, wrote the following on the planetary model proposed by Ibn Bajjah (Avempace):

"I have heard that Abu Bakr [Ibn Bajja] discovered a system in which no epicycles occur, but eccentric spheres are not excluded by him. I have not heard it from his pupils; and even if it be correct that he discovered such a system, he has not gained much by it, for eccentricity is likewise contrary to the principles laid down by Aristotle.... I have explained to you that these difficulties do not concern the astronomer, for he does not profess to tell us the existing properties of the spheres, but to suggest, whether correctly or not, a theory in which the motion of the stars and planets is uniform and circular, and in agreement with observation."^[91]

Ibn Bajjah also proposed the Milky Way galaxy to be made up of many stars but that it appears to be a continuous image due to the effect of refraction in the Earth's atmosphere, citing his observation of the conjunction of Jupiter and Mars in 500 AH (1106/1107 AD) as evidence.^[58]

In Toledo, Muladi astronomer Al-Zarqali (1029–1087) wrote further on the Tables of Toledo. His works were carried out by Ibn al-Kammad and confirmed by Ibn al‐Haim al‐Ishbili.

Maragha School

The "Maragha school" was an astronomical tradition beginning in the Maragheh observatory and continuing with astronomers from the Damascus mosque and Samarkand observatory. Like their Andalusian predecessors, the Maragha astronomers attempted to solve the equant problem and produce alternative configurations to the Ptolemaic model. They were more successful than their Andalusian predecessors in producing non-Ptolemaic configurations which eliminated the equant and eccentrics, were more accurate than the Ptolemaic model in numerically predicting planetary positions, and were in better agreement with empirical observations.^[92] The most important of the Maragha astronomers included Mo'ayyeduddin Urdi (d. 1266), Nasīr al-Dīn al-Tūsī (1201–1274), Najm al-Dīn al-Qazwīnī al-Kātibī (d. 1277), Qotb al-Din Shirazi (1236–1311), Sadr al-Sharia al-Bukhari (c. 1347), Ibn al-Shatir (1304–1375), Ali al-Qushji (c. 1474), al-Birjandi (d. 1525) and Shams al-Din al-Khafri (d. 1550).^[93]

Nasīr al-Dīn al-Tūsī resolved significant problems in the Ptolemaic system with the Tusi-couple, which later played an important role in the Copernican model.

Some have described their achievements in the 13th and 14th centuries as a "Maragha Revolution", "Maragha School Revolution", or "Scientific Revolution before the Renaissance". An important aspect of this revolution included the realization that astronomy should aim to describe the behavior of physical bodies in mathematical language, and should not remain a mathematical hypothesis, which would only save the phenomena. The Maragha astronomers also realized that the Aristotelian view of motion in the universe being only circular or linear was not true, as the Tusi-couple showed that linear motion could also be produced by applying circular motions only.^[94]

Unlike the ancient Greek and Hellenistic astronomers who were not concerned with the coherence between the mathematical and physical principles of a planetary theory, Islamic astronomers insisted on the need to match the mathematics with the real world surrounding them,^[95] which gradually evolved from a reality based on Aristotelian physics to one based on an empirical and mathematical physics after the work of Ibn al-Shatir. The Maragha Revolution was thus characterized by a shift away from the philosophical foundations of Aristotelian cosmology and Ptolemaic astronomy and towards a greater emphasis on the empirical observation and mathematization of astronomy and of nature in general, as exemplified in the works of Ibn al-Shatir, al-Qushji, al-Birjandi and al-Khafri.^[96][97][98]

Ibn al-Shatir's model for the appearances of Mercury, showing the multiplication of epicycles using the Tusi-couple, thus eliminating the Ptolemaic eccentrics and equant.

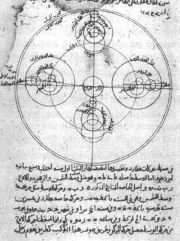
Other achievements of the Maragha school include the first empirical observational evidence for the Earth's rotation on its axis by al-Tusi and al-Qushji,^[15] the separation of natural philosophy from astronomy by Ibn al-Shatir and al-Qushji,^[16] the rejection of the Ptolemaic model on empirical rather than philosophical grounds by Ibn al-Shatir,^[92] and the development of a non-Ptolemaic model by Ibn al-Shatir that was mathematically identical to the heliocentric Copernical model.^[99]

Mo'ayyeduddin Urdi (d. 1266) was the first of the Maragheh astronomers to develop a non-Ptolemaic model, and he proposed a new theorem, the "Urdi lemma".^[100] Nasīr al-Dīn al-Tūsī (1201–1274) resolved significant problems in the Ptolemaic system by developing the Tusi-couple as an alternative to the physically problematic equant introduced by Ptolemy.^[101] Tusi's student Qotb al-Din Shirazi (1236–1311), in his The Limit of Accomplishment concerning Knowledge of the Heavens, discussed the possibility of heliocentrism. Al-Qazwīnī al-Kātibī (d. 1277), who also worked at the Maragheh observatory, in his Hikmat al-'Ain, wrote an argument for a heliocentric model, though he later abandoned the idea.^[83]

Medieval manuscript by Qutb al-Din al-Shirazi depicting an epicyclic planetary model.

Ibn al-Shatir (1304–1375) of Damascus, in A Final Inquiry Concerning the Rectification of Planetary Theory, incorporated the Urdi lemma, and eliminated the need for an equant by introducing an extra epicycle (the Tusi-couple), departing from the Ptolemaic system in a way that was mathematically identical to what Nicolaus Copernicus did in the 16th century. Unlike previous astronomers before him, Ibn al-Shatir was not concerned with adhering to the theoretical principles of natural philosophy or Aristotelian cosmology, but rather to produce a model that was more consistent with empirical observations. For example, it was Ibn al-Shatir's concern for observational accuracy which led him to eliminate the epicycle in the Ptolemaic solar model and all the eccentrics, epicycles and equant in the Ptolemaic lunar model. His model was thus in better agreement with empirical observations than any previous model,^[92] and was also the first that permitted empirical testing.^[102] His work thus marked a turning point in astronomy, which may be considered a "Scientific Revolution before the Renaissance".^[92] His rectified model was later adapted into a heliocentric model by Copernicus,^[101] which was mathematically achieved by reversing the direction of the last vector connecting the Earth to the Sun.^[5] In the published version of his masterwork, De revolutionibus orbium coelestium, Copernicus also cites the theories of al-Battani, Arzachel and Averroes as influences,^[85] while the works of Ibn al-Haytham and al-Biruni were also known in Europe at the time.

An area of active discussion in the Maragheh school, and later the Samarkand and Istanbul observatories, was the possibility of the Earth's rotation. Supporters of this theory included Nasīr al-Dīn al-Tūsī, Nizam al-Din al-Nisaburi (c. 1311), al-Sayyid al-Sharif al-Jurjani (1339–1413), Ali al-Qushji (d. 1474), and Abd al-Ali al-Birjandi (d. 1525). Al-Tusi was the first to present empirical observational evidence of the Earth's rotation, using the location of comets relevant to the Earth as evidence, which al-Qushji elaborated on with further empirical observations while rejecting Aristotelian natural philosophy altogether. Both of their arguments were similar to the arguments later used by Nicolaus Copernicus in 1543 to explain the Earth's rotation (see Astronomical physics and Earth's motion section below).^[15]

However, it remains a fact that the Maragha school never made the big leap to heliocentrism.^[103] In addition, the influence of the Maragha school on Copernicus remains speculative, since there is no documentary evidence to prove it. The possibility that Copernicus independently developed the Tusi couple remains open, since no researcher has yet proven that he knew about Tusi´s work or the Maragha school.^[103][104] It has been argued that, given some differences between the two models, it is more likely that Copernicus could have taken the ideas found in the Tusi couple from Proclus's Commentary on the First Book of Euclid.^[105] Another possible source for Copernicus's knowledge is the Questiones de Spera of Nicole Oresme, who described how a reciprocating linear motion of a celestial body could be produced by a combination of circular motions similar to those proposed by al-Tusi.^[106]

Multiversal cosmology

Fakhr al-Din al-Razi (1149–1209), in dealing with his conception of physics and the physical world in his Matalib, discusses Islamic cosmology and astronomy. He criticizes the idea of the Earth's centrality within the universe and "explores the notion of the existence of a multiverse in the context of his commentary" on the Qur'anic verse, "All praise belongs to God, Lord of the Worlds." He raises the question of whether the term "worlds" in this verse refers to "multiple worlds within this single universe or cosmos, or to many other universes or a multiverse beyond this known universe." In volume 4 of the Matalib, Al-Razi states:^[17]

It is established by evidence that there exists beyond the world a void without a terminal limit (khala' la nihayata laha), and it is established as well by evidence that God Most High has power over all contingent beings (al-mumkinat). Therefore He the Most High has the power (qadir) to create a thousand thousand worlds (alfa alfi 'awalim) beyond this world such that each one of those worlds be bigger and more massive than this world as well as having the like of what this world has of the throne (al-arsh), the chair (al-kursiyy), the heavens (al-samawat) and the earth (al-ard), and the sun (al-shams) and the moon (al-qamar). The arguments of the philosophers (dala'il al-falasifah) for establishing that the world is one are weak, flimsy arguments founded upon feeble premises.

Al-Razi rejected the Aristotelian and Avicennian view of the impossibility of multiple worlds or universes. He describes the main Aristotelian arguments against the existence of multiple worlds or universes, pointing out their weaknesses and refuting them. This rejection arose from his affirmation of atomism, as advocated by the Ash'ari school of Islamic theology, which entails the existence of vacant space in which the atoms move, combine and separate. He discussed more on the issue of the void in greater detail in volume 5 of the Matalib.^[17] He argued that God has the power to fill the vacuum with an infinite number of universes.^[107]

Observational astronomy

An Arabic manuscript from the 13th century depicting Astronomers

The transit of Venus and transit of Mercury were claimed to have been observed by medieval Islamic astronomers. In the 11th century, the Persian polymath Avicenna claimed to have observed the transit of Venus across the Sun. He took this as evidence that Venus was, at least sometimes, below the Sun (in the Ptolemaic cosmology).^[108] In the 12th century, the Andalusian astronomer Ibn Bajjah reported observing "the two planets as black spots on the face of the Sun." In the 13th century, the Maragha astronomer Qotb al-Din Shirazi identified to Ibn Bajjah's observation as the transit of Venus and Mercury.^[109] However, Ibn Bajjah cannot have observed a Venus transit, as there were no Venus transits in his lifetime.^[110]

The astronomical tradition established by the Maragha school continued at the Ulugh Beg Observatory at Samarkand, in modern-day Uzbekistan. Founded by Ulugh Beg in the early 15th century, the observatory made considerable progress in observational astronomy. In the Zij-i Sultani, Beg determined the length of the sidereal year as 365^d 5^h 49^m 15^s, which has an error of +25^s, making it more accurate than Nicolaus Copernicus' estimate which had an error of +30^s. Beg also determined the Earth's axial tilt as 23.52 degrees, which remains the most accurate measurement to date. It was more accurate than later measurements by Copernicus and Tycho Brahe, and matches the currently accepted value precisely.^[111]

Islamic astronomy in the Far East

Muslim astronomers were brought to China in order to work on calendar making and astronomy since the Abbasid period the first major introduction of Islamic Mathematics and Astronomy occurred during the Song dynasty.

Ma Yize (ca. 910 - 1005) was an important Chinese Muslim (Hui), Islamic astronomer and astrologist who worked as the chief official of the astronomical observatory for the Song dynasty. In the early 10th Century, the Chinese emperor of the Song dynasty encouraged the advancement of the study of astronomy and its related disciplines. In 961, the Emperor Taizu (r. 960-976) appointed Ma Yize (910?-1005) as the chief official to take charge of the government observatory. After compiling several important astrological works, including the Yingtianli (Calendar of Corresponding Heavens). His job was to provide observation, and computation of the regularities in celestial phenomena, using the Islamic methods. His findings were used by Wang Chuna in the compilation of Yingtianli, which was completed in 963. The calculation, based on a 7-day week system similar to that in the Islamic calendar, was first adopted in this document, which was the most important occurrence in the Chinese history of calendrical methods.

Ma Yize might have consulted many works of Islamic mathematical astronomy into Chinese, including:

• Kitab al-Zij, 880, by Abu'Abdallah al-Battani (858-929)
• al-Zij al-sabi, The Sabian Tables
• Kitab Matali' al-Buruj, On the Ascensions of the Signs of the Zodiac
• Kitab Aqdar al- Ittisalat, On the Quantities of the Astrological Applications

It is possible that Ma was influenced by Al-Battani and Al-Hamdani. Owing to Ma's contribution to the compilation of 'Yingtianli', Ma was made a hereditary noble and his sons later succeeded his position with the Imperial Observatory.

During Mongol Yuan Dynasty,^{[112][113][114]} The Chinese scholar Yeh-lu Chu'tsai accompanied Genghis Khan to Persia in 1210 and studied their calendar for use in the Mongol Empire.^[113] Kublai Khan brought Iranians to Beijing to construct an observatory and an institution for astronomical studies.^[112]

Several Chinese astronomers worked at the Maragheh observatory, founded by Nasir al-Din al-Tusi in 1259 under the patronage of Hulagu Khan in Persia.^[115] One of these Chinese astronomers was Fu Mengchi, or Fu Mezhai.^[116] In 1267, the Persian astronomer Jamal ad-Din, who previously worked at Maragha observatory, presented Kublai Khan with seven Persian astronomical instruments, including a terrestrial globe and an armillary sphere,^[117] as well as an astronomical almanac, which was later known in China as the Wannian Li ("Ten Thousand Year Calendar" or "Eternal Calendar"). He was known as "Zhamaluding" in China, where in 1271,^[116] he was appointed by Khan as the first director of the Islamic observatory in Beijing,^[115] known as the Islamic Astronomical Bureau, which operated alongside the Chinese Astronomical Bureau for four centuries. Islamic astronomy gained a good reputation in China for its theory of planetary latitudes, which did not exist in Chinese astronomy at the time, and for its accurate prediction of eclipses.^[116]

Some of the astronomical instruments constructed by the famous Chinese astronomer Guo Shoujing shortly afterwards resemble the style of instrumentation built at Maragheh.^[115] In particular, the "simplified instrument" (jianyi) and the large gnomon at the Gaocheng Astronomical Observatory show traces of Islamic influence.^[118] While formulating the Shoushili calendar in 1281, Shoujing's work in spherical trigonometry may have also been partially influenced by Islamic mathematics, which was largely accepted at Kublai's court.^[119] These possible influences include a pseudo-geometrical method for converting between equatorial and ecliptic coordinates, the systematic use of decimals in the underlying parameters, and the application of cubic interpolation in the calculation of the irregularity in the planetary motions.^[118]

Around 1384 during the Ming Dynasty, Emperor Zhu Yuanzhang ordered the Chinese translation and compilation of Islamic astronomical tables, a task that was carried out by the scholars Mashayihei, a Muslim astronomer, and Wu Bozong, a Chinese scholar-official. These tables came to be known as the Huihui Lifa (“Muslim System of Calendrical Astronomy”), which was published in China a number of times until the early 18th century,^[120] though the Qing Dynasty had officially abandoned the science of Astronomy in 1659.^[121] A Korean translation of the Huihui Lifa was also studied in Korea under the Joseon Dynasty during the time of Sejong the Great in the 15th century.^[122] The tradition of Chinese-Islamic astronomy survived in Korea for even longer, up until the early 19th century.^[121]

Islamic astronomy in Christian Europe

Astrolabic quadrant, England, 1388.

During this period, Islamic-ruled regions of Europe, such as Al-Andalus, the Emirate of Sicily, and southern Italy, were slowly being reconquered by Christians. This led to the Arabic-Latin translation movement, which saw the assimilation of knowledge from the Islamic world by Western European science, including astronomy.^[5]

One of the most productive translators in Spain was Gerard of Cremona, who translated 87 books from Arabic to Latin. The astronomical texts he translated include Jabir ibn Aflah's Elementa astronomica,^[123] Ahmad ibn Muhammad ibn Kathīr al-Farghānī's On Elements of Astronomy on the Celestial Motions,^[124] the works of Thabit ibn Qurra and Hunayn ibn Ishaq,^[125] and the works of Arzachel, the Banū Mūsā brothers, Abū Kāmil Shujā ibn Aslam, Abu al-Qasim, and Ibn al-Haytham (including the Book of Optics).^[44] The astronomical works translated by Plato of Tivoli included Al-Battani's astronomical and trigonometrical work De motu stellarum. Al-Khwarizmi's Astronomical tables (also containing trigonometric tables) were translated by Robert of Chester^[123] and by Adelard of Bath (fl. 1116-1142), who also translated the Introduction to Astrology of Abū Ma'shar.^[126] Adelard associated with other scholars in Western England such as Peter Alfonsi and Walcher of Malvern who translated and developed the astronomical concepts brought from Islamic Spain.^[127] Other Arabic astronomical texts translated into Latin include Muhammad al-Fazari's Great Sindhind (based on the Surya Siddhanta and the works of Brahmagupta).^[128]

In addition to the Arabic-Latin translation movement in Western Europe, Byzantine astronomers also translated Arabic texts on astronomy into Medieval Greek during this time. In particular, Gregory Choniades, who had visited the famous Maragheh observatory, translated various Arabic books on astronomy, including for example the works of Abu Ma'shar, Ibn Yunus, Al-Khazini (who was of Byzantine Greek descent but raised in a Persian culture),^[129] Al-Khwārizmī^[130] and Nasīr al-Dīn al-Tūsī (such as the Zij-i Ilkhani and other Zij treatises) among others.^[4] Byzantine science thus played an important role in transmitting Arabic knowledge to Western Europe in later centuries, such as the transmission of the Tusi-couple, which later appeared in the work of Nicolaus Copernicus.^[4][5]

1450-1900

This period was considered the period of stagnation, when the traditional system of astronomy continued to be practised with enthusiasm, but with decreasing innovation.^[27] It was believed there was no innovation of major significance during this period, but this view has been rejected by historians of astronomy in recent times, who argue that Muslim astronomers continued to make significant advances in astronomy through to the 16th century and possibly after this as well.^[16][131] After the 16th century, there appears to have been little concern for theoretical astronomy, but observational astronomy in the Islamic tradition continued in the three Muslim gunpowder empires: the Ottoman Empire, the Safavid dynasty of Persia, and the Mughal Empire of India.

Astronomical physics and Earth's motion

Ali al-Qushji provided empirical evidence for the Earth's motion and developed an astronomical physics independent from Aristotelian physics and natural philosophy.

The work of Ali al-Qushji (d. 1474), who worked at Samarkand and then Istanbul, is seen as a late example of innovation in Islamic theoretical astronomy and it is believed he may have possibly had some influence on Nicolaus Copernicus due to similar arguments concerning the Earth's rotation. Before al-Qushji, the only astronomer to present empirical evidence for the Earth's rotation was Nasīr al-Dīn al-Tūsī (d. 1274), who used the phenomena of comets to refute Ptolemy's claim that a stationery Earth can be determined through observation. Al-Tusi, however, eventually accepted that the Earth was stationery on the basis of Aristotelian cosmology and natural philosophy. By the 15th century, the influence of Aristotelian physics and natural philosophy was declining due to religious opposition from Islamic theologians such as Al-Ghazali who opposed to the interference of Aristotelianism in astronomy, opening up possibilities for an astronomy unrestrained by philosophy. Under this influence, Al-Qushji, in his Concerning the Supposed Dependence of Astronomy upon Philosophy, rejected Aristotelian physics and completely separated natural philosophy from astronomy, allowing astronomy to become a purely empirical and mathematical science. This allowed him to explore alternatives to the Aristotelian notion of a stationery Earth, as he explored the idea of a moving Earth. He also observed comets and elaborated on al-Tusi's argument. He took it a step further and concluded, on the basis of empirical evidence rather than speculative philosophy, that the moving Earth theory is just as likely to be true as the stationary Earth theory and that it is not possible to empirically deduce which theory is true.^{[15][16][132]}

His predecessor al-Tusi had previously realized that "the monoformity of falling bodies, and the uniformity of celestial motions," both moved “in a single way,” though he still relied on Aristotelian philosophy to provide "certain principles that only the natural philosophers could provide the astronomer." Qushji took this concept further and proposed that "the astronomer had no need for Aristotelian physics and in fact should establish his own physical principles independently of the natural philosophers." Alongside his rejection of Aristotle's concept of a stationary Earth,^[133] Qushji also rejected the Aristotelian notion of the heavenly bodies moving in uniform circular motion.^[134] His work was an important step away from Aristotelian physics and towards an independent astronomical physics.^[135] This is considered to be a "conceptual revolution"^[135][136] that had no precedent in European astronomy prior to the Copernican Revolution in the 16th century.^[137] Despite the similarity in their discussions regarding the Earth's motion, there is uncertainty over whether al-Qushji had any influence on Copernicus. However, it is likely that they both may have arrived at similar conclusions due to using the earlier work of al-Tusi as a basis. This is more of a possibility considering "the remarkable coincidence between a passage in De revolutionibus (I.8) and one in Ṭūsī’s Tadhkira (II.1[6]) in which Copernicus follows Ṭūsī’s objection to Ptolemy’s “proofs” of the Earth’s immobility." This can be considered as evidence that not only was Copernicus influenced by the mathematical models of Islamic astronomers, but may have also been influenced by the astronomical physics they began developing and their views on the Earth's motion.^[138]

In the 16th century, the debate on the Earth's motion was continued by Al-Birjandi (d. 1528), who in his analysis of what might occur if the Earth were moving, develops a hypothesis similar to Galileo Galilei's notion of "circular inertia",^[139] which he described in the following observational test (as a response to one of Qutb al-Din al-Shirazi's arguments):

"The small or large rock will fall to the Earth along the path of a line that is perpendicular to the plane (sath) of the horizon; this is witnessed by experience (tajriba). And this perpendicular is away from the tangent point of the Earth’s sphere and the plane of the perceived (hissi) horizon. This point moves with the motion of the Earth and thus there will be no difference in place of fall of the two rocks."^[140]

Planetary theory

A manuscript written during the Abbasid Era.

It was traditionally believed that Islamic astronomers made no more advances in planetary theory after the work of Ibn al-Shatir in the 14th century, but recent studies have shown that there were several significant advances in planetary theory through to the 16th century. Ali Qushji, for example, improved on al-Tusi's planetary model and presented an alternative planetary model for Mercury.^[141] He also rejected the Aristotelian notion of the planets moving in uniform circular motion.^[134] George Saliba also studied the works of a 16th century astronomer, Shams al-Din al-Khafri (d. 1550), a Safavid commentator on earlier Maragha astronomers. Saliba wrote the following on al-Khafri's work:

By his sheer insight into the role of mathematics in describing natural phenomena, this astronomer managed to bring the hay'a tradition to such unparalleled heights that could not be matched anywhere else in the world at that time neither mathematically nor astronomically. By working on the alternative mathematical models that could replace those of Ptolemy, and by scrutinizing the works of his predecessors who were all searching for unique mathematical models that could describe the physical phenomena consistently, this astronomer finally realized that all mathematical modeling had no physical truth by itself and was simply another language with which one could describe the physical observed reality. He also realized that the specific phenomena that were being described by the Ptolemaic models did not have unique mathematical solutions that were subject to the same restraints. Rather there were several mathematical models that could account for the Ptolemaic observations, yield identical predictive results at the same critical points used by Ptolemy to construct his own models (thus accounting for the observations as perfectly as Ptolemy could) and still meet the consistency requirement that was imposed by the Aristotelian cosmology which was adopted by the writers in the hay'a tradition.^[131]

A model of the heliocentric system attributed to Nicolaus Copernicus.

Ottoman observational astronomy

Another notable 16th century Muslim astronomer was the Ottoman astronomer Taqi al-Din, who built the Istanbul observatory of Taqi al-Din in 1577, where he carried out astronomical observations until 1580. He produced a Zij (named Unbored Pearl) and astronomical catalogues that were more accurate than those of his contemporaries, Tycho Brahe and Nicolaus Copernicus. Taqi al-Din was also the first astronomer to employ a decimal point notation in his observations rather than the sexagesimal fractions used by his contemporaries and predecessors.^[142] He also invented a variety of astronomical instruments, including accurate mechanical astronomical clocks from 1556 to 1580.

After the destruction of the Istanbul observatory of Taqi al-Din in 1580, astronomical activity stagnated in the Ottoman Empire, until the introduction of Copernican heliocentrism in 1660, when the Ottoman scholar Ibrahim Efendi al-Zigetvari Tezkireci translated Noël Duret's French astronomical work (written in 1637) into Arabic.^[143]

Islamic astronomy in India

In the Mughal Empire, the 16th and 17th centuries saw a synthesis between Islamic and Indian astronomy, where Islamic observational techniques and instruments were combined with Hindu computational techniques. While there appears to have been little concern for theoretical astronomy, Muslim and Hindu astronomers in India continued to make advances in observational astronomy and produced nearly a hundred Zij treatises. Humayun built a personal observatory near Delhi, while Jahangir and Shah Jahan were also intending to build observatories but were unable to do so. After the decline of the Mughal Empire, however, it was a Hindu king, Jai Singh II of Amber, who attempted to revive the Islamic tradition of astronomy in India. In the early 18th century, he built several large observatories called Yantra Mandirs in order to rival the famous Samarkand observatory, and in order to update Ulugh Beg's Zij-i-Sultani with more accurate observations. The instruments and observational techniques used at the observatory were mainly derived from the Islamic tradition, and the computational techniques from the Hindu tradition.^[144][145] In particular, one of the most remarkable astronomical instruments invented by Muslims in Mughal India is the seamless celestial globe (see Globes below).

Jai Singh also invited European Jesuit astronomers to his observatory, who had bought back the astronomical tables compiled by Philippe de La Hire in 1702. After examining La Hire's work, Jai Singh concluded that the techniques and instruments used in the European tradition were inferior to the Islamic and Indian traditions. It is uncertain whether Islamic astronomers in India were aware of the Copernican Revolution via the Jesuits, but it appears they were not concerned with theoretical astronomy, hence the theoretical advances in Europe did not interest them at the time.^[146] They did, however, employ the use of telescopes. In the Zij-i Muhammad Shahi, Jai Singh states: "telescopes were constructed in my kingdom and using them a number of observations were carried out."^[147]

Following the arrival of the British East India Company in the 18th century, Islamic astronomy was slowly displaced by European astronomy, though there were attempts at harmonizing the two traditions. For example, the Indian Islamic scholar Mir Muhammad Hussain had travelled to England in 1774 to study Western science and, on his return to India in 1777, he wrote a Persian treatise on astronomy. He wrote about the heliocentric model, and argued that there exists an infinite number of universes (awalim), each with their own planets and stars, and that this demonstrates the omnipotence of God, who is not confined to a single universe. Hussain's idea of a universe resembles the modern concept of a galaxy, thus his view corresponds to the modern view that the universe consists of billions of galaxies, each one consisting of billions of stars.^[148] The last known Zij treatise was the Zij-i Bahadurkhani, written in 1838 by the Indian astronomer Ghulam Hussain Jaunpuri (1760–1862) and printed in 1855, dedicated to Bahadur Khan. The treatise incorporated the heliocentric system into the Zij tradition.^[149]

Observatories

Islamic astronomers had based their work largely on actual observations of the heavens, far more so than earlier Greek astronomers who relied heavily upon abstract calculation.^[150] This led to the emergence of the modern astronomical observatory as a research institute^[151] (as opposed to a private observation post as was the case in ancient times)^[152] being first introduced by medieval Muslim astronomers, who produced accurate Zij treatises using these observatories. The Islamic observatory was the first specialized astronomical institution with its own scientific staff,^[151] director, astronomical program,^[152] large astronomical instruments, and building where astronomical research and observations are carried out. Islamic observatories were also the first to employ enormously large astronomical instruments in order to greatly improve the accuracy of their observations.^[151]

The medieval Islamic observatories were also the earliest institutions to emphasize group research (as opposed to individual research) and where "theoretical investigations went hand in hand with observations." In this sense, they were similar to modern scientific research institutions.^[153]

Early observatories

The first systematic observations in Islam are reported to have taken place under the patronage of al-Ma'mun, and the first Islamic observatories were built in 9th century Iraq under his patronage. In many private observatories from Damascus to Baghdad, meridian degrees were measured, solar parameters were established, and detailed observations of the Sun, Moon, and planets were undertaken. One of these early observatories in Baghdad was the Al-Shammisiyyah observatory, where between 825 to 835, Habash al-Hasib al-Marwazi conducted various observations and estimated a number of geographic and astronomical values.^[35]

In the 10th century, the Buwayhid dynasty encouraged the undertaking of extensive works in Astronomy, such as the construction of a large scale instrument with which observations were made in the year 950. We know of this by recordings made in the zij of astronomers such as Ibn al-Alam. The great astronomer Abd Al-Rahman Al Sufi was patronised by prince 'Adud al-Dawla, who systematically revised Ptolemy's catalogue of stars. Abu-Mahmud al-Khujandi also constructed an observatory in Ray, Iran where he is known to have constructed the first huge mural sextant in 994 AD.^[154] Sharaf al-Daula also established a similar observatory in Baghdad. Reports by Ibn Yunus and al-Zarqall in Toledo and Cordoba indicate the use of sophisticated instruments for their time.

Current status of Maragheh observatory.

It was Malik Shah I who established the first large observatory, probably in Isfahan. It was here where Omar Khayyám with many other collaborators constructed a zij and formulated the Persian solar calendar, a.k.a. the jalali calendar, the most accurate solar calendar to date. A modern version of this calendar is still in official use in Iran today.

Late medieval observatories

The more influential observatories, however, were established beginning in the 13th century. The Maragheh observatory was founded by Nasīr al-Dīn al-Tūsī under the patronage of Hulegu Khan in the 13th century. Here, al-Tusi supervised its technical construction at Maragheh. The facility contained resting quarters for Hulagu Khan, as well as a library and mosque. Some of the top astronomers of the day gathered there, and their collaboration resulted in important alternatives to the Ptolemaic model over a period of 50 years. The observations of al-Tusi and his team of researchers were compiled in the Zij-i Ilkhani.

Ulugh Beg, founder of the large Ulugh Beg Observatory in Samarkand, honored on this Soviet stamp.

In 1420, prince Ulugh Beg, himself an astronomer and mathematician, founded another large observatory, the Ulugh Beg Observatory, in Samarkand. The remains of the observatory were excavated in 1908 by Russian teams. Ulugh Beg, alongside his team of researchers that included Jamshīd al-Kāshī and Ali Qushji, compiled the results of their observations in the Zij-i-Sultani (1437).

Istanbul observatory of Taqi al-Din in 1577.

In 1577, Taqi al-Din Muhammad ibn Ma'ruf founded a large observatory in Istanbul. This was on the same scale as those in Maragha and Samarkand as well as that of his contemporary Tycho Brahe.

In the Mughal Empire, Humayun built a personal observatory near Delhi in the 16th century, while Jahangir and Shah Jahan were also intending to build observatories but were unable to do so. After the decline of the Mughal Empire, the Hindu king Jai Singh II of Amber built several large observatories called Yantra Mandirs inspired by the famous Samarkand observatory. The instruments and observational techniques used at the observatory were mainly derived from the Islamic tradition, and the computational techniques from the Hindu tradition.^[144][145]

Instruments

A Persian (Iranian) astrolabe from 1208.

Modern knowledge of the instruments used by Muslim astronomers primarily comes from two sources. First the remaining instruments in private and museum collections today, and second the treatises and manuscripts preserved from the Middle Ages.

Muslims both made many improvements to instruments already in use before their time, such as adding new scales or details and significantly enlarging them to improve accuracy,^[111] and invented many of their own new instruments. Islamic astronomers were also the first to build enormously large scientific instruments in order to greatly improve the accuracy of observations.^[151] Their contributions to astronomical instrumentation are abundant. Many of these instruments were often invented or designed for Islamic purposes, such as the determination of the Qibla (direction to Mecca) or the times of Salah prayers.

Astrolabes and planisphere

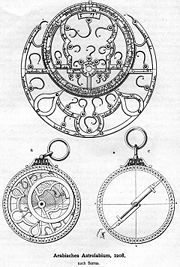
Brass astrolabes were developed in much of the Islamic world, often as an aid to finding the qibla. The earliest known example is dated 315 AH, (927/8 CE). The first person credited for building the Astrolabe in the Islamic world is reportedly Fazari.^[155] Though the first astrolabe to chart the stars was invented in the Hellenistic civilization, Fazari made several improvements to the device, such as the introduction of angular scales to the astrolabe,^[156] adding circles indicating azimuths on the horizon.^[157] The Arabs then took it during the Abbasid Caliphate and perfected it to be used to find the beginning of Ramadan, the hours of prayer (Salah), the direction of Mecca (Qibla), and over a thousand other uses. In the 10th century, Al-Sufi first described over 1,000 different uses of an astrolabe, in areas as diverse as astronomy, astrology, horoscopes, navigation, surveying, timekeeping, Qibla, Salah, etc.

Large astrolabe

Ibn Yunus in the 10th century accurately observed more than 10,000 entries for the sun's position for many years using a large astrolabe with a diameter of nearly 1.4 meters.^[44]

Mechanical geared astrolabe

The first mechanical astrolabes with gears were invented in the Muslim world, and were perfected by Ibn Samh (c. 1020). One such device with eight gear-wheels was also constructed by Abū Rayhān al-Bīrūnī in 996. These can be considered as an ancestor of the mechanical clocks developed by later Muslim engineers.^[158]

An 18th century Persian astrolabe, kept at The Whipple Museum of the History of Science in Cambridge, England.

Orthographical astrolabe

Abu Rayhan al-Biruni invented and wrote the earliest treatise on the orthographical astrolabe in the 11th century.

An astrolabe from Al-Andalus dating back to 1067.

Universal astrolabe (Saphaea)

The first astrolabe instruments were used to read the rise of the time of rise of the Sun and fixed stars. The first universal astrolabes were later constructed in the Islamic world and which, unlike their predecessors, did not depend on the latitude of the observer and could be used anywhere on the Earth. The basic idea for a latitude-independent astrolabe was conceived in the 9th century by Habash al-Hasib al-Marwazi in Baghdad and the topic was later discussed in the early 11th century by Al-Sijzi in Persia.^[159]

The first known universal astrolabe to be constructed was by Ali ibn Khalaf al-Shakkaz, an Arabic herbalist or apothecary in 11th century Al-Andalus. His instrument could solve problems of spherical astronomy for any geographic latitude, though in a somewhat more complicated fashion than the standard astrolabe. Another, more advanced and more famous, universal astrolabe was constructed by Abū Ishāq Ibrāhīm al-Zarqālī (Arzachel) soon after. His instrument became known in Europe as the "Saphaea".^[160] It was a universal lamina (plate) which "constituted a universal device representing a stereographic projection for the terrestrial equator and could be used to solve all the problems of spherical astronomy for any latitude."^[161]

Zuraqi

The Zuraqi is a unique astrolabe invented by Al-Sijzi for a heliocentric planetary model in which the Earth is moving rather than the sky.^[162]

The planisphere was invented by Abū Rayhān al-Bīrūnī.

Planisphere

In the early 11th century, Abū Rayhān al-Bīrūnī invented and wrote the first treatise on the planisphere, which was an early analog computer.^[163] The astrolabe was a predecessor of the modern planisphere.

Linear astrolabe

A famous work by Sharaf al-Dīn al-Tūsī is one in which he describes the linear astrolabe, sometimes called the "staff of al-Tusi", which he invented.^[164]

Analog computers

Various analog computer devices were invented to compute the latitudes of the Sun, Moon, and planets, the ecliptic of the Sun, the time of day at which planetary conjunctions will occur, and for performing linear interpolation.

Equatorium

The Equatorium was an analog computer invented by Abū Ishāq Ibrāhīm al-Zarqālī (Arzachel) in al-Andalus, probably around 1015 CE. It is a mechanical device for finding the longitudes and positions of the Moon, Sun, and planets, without calculation using a geometrical model to represent the celestial body's mean and anomalistic position.^[165]

Mechanical geared calendar computer

Abu Rayhan Biruni also invented the first mechanical lunisolar calendar computer which employed a gear train and eight gear-wheels.^[166] This was an early example of a fixed-wired knowledge processing machine.^[167]

Volvelle

The volvelle, also called a wheel chart, is a type of slide chart, paper constructions with rotating parts. It is considered an early example of a paper analog computer.^[168] The volvelle can be traced back to "certain Arabic treateses on humoral medicine"^[169] and to Biruni (c. 1000) who made important contributions to the development of the volvelle.^[170] In the 20th century, the volvelle had many diverse uses.

The torquetum was invented by Jabir ibn Aflah (Geber).

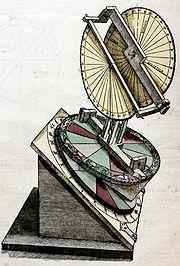
Torquetum

Jabir ibn Aflah (Geber) (c. 1100-1150) invented the torquetum, an observational instrument and mechanical analog computer device used to transform between spherical coordinate systems.^[171] It was designed to take and convert measurements made in three sets of coordinates: horizon, equatorial, and ecliptic.

Castle clock with programmable analog computer

In 1206, Al-Jazari invented his largest astronomical clock, the "castle clock".^[172] It displayed the zodiac and the solar and lunar orbits. Another innovative feature of the clock was a pointer which traveled across the top of a gateway and caused automatic doors to open every hour.^[173]

Mechanical astrolabe with geared calendar computer

In 1235, Abi Bakr of Isfahan invented a brass astrolabe with a geared calendar movement based on the design of Abū Rayhān al-Bīrūnī's mechanical calendar computer.^[174] Abi Bakr's geared astrolabe uses a set of gear-wheels and is the oldest surviving complete mechanical geared machine in existence.^[175][176]

Plate of Conjunctions

In the 15th century, al-Kashi invented the Plate of Conjunctions, a computing instrument used to determine the time of day at which planetary conjunctions will occur,^[177] and for performing linear interpolation.^[178]

Planetary computer

In the 15th century, al-Kashi also invented a mechanical planetary computer which he called the Plate of Zones, which could graphically solve a number of planetary problems, including the prediction of the true positions in longitude of the Sun and Moon,^[178] and the planets in terms of elliptical orbits;^[179] the latitudes of the Sun, Moon, and planets; and the ecliptic of the Sun. The instrument also incorporated an alhidade and ruler.^[180]

Astronomical clocks

The Muslims constructed a variety of astronomical clocks for use in their observatories.^[181]

Water-powered astronomical clocks

Al-Jazari devised monumental water-powered astronomical clocks which displayed moving models of the Sun, Moon, and stars. His largest astronomical clock was the "castle clock".^[172]

Mechanical observational clock

Taqi al-Din invented the "observational clock", which he described as "a mechanical clock with three dials which show the hours, the minutes, and the seconds." This was the first clock to measure time in seconds, and he used it for astronomical purposes, specifically for measuring the right ascension of the stars. This is considered one of the most important innovations in 16th-century practical astronomy, as previous clocks were not accurate enough to be used for astronomical purposes.^[142] He further improved the observational clock, as described in his Sidrat al-muntaha, using only one dial to represent the hours, minutes and seconds. He describes this observational clock as "a mechanical clock with a dial showing the hours, minutes and seconds and we divided every minute into five seconds."^[182]

Dials

Muslim astronomers and engineers invented a variety of dials for timekeeping, and for determining the times of the five daily prayers.

Sundials

Muslims made several important improvements to the theory and construction of sundials, which they inherited from their Indian and Hellenistic predecessors. Al-Khwarizmi made tables for these instruments which considerably shortened the time needed to make specific calculations. Sundials were frequently placed on mosques to determine the time of prayer. One of the most striking examples was built in the 14th century by the muwaqqit (timekeeper) of the Umayyad Mosque in Damascus, Ibn al-Shatir.^[183] Muslim astronomers and engineers were the first to write instructions on the construction of vertical sundials and polar sundials.^[184]

Since ancient dials were nodus-based with straight hour-lines, they indicated unequal hours — also called temporary hours — that varied with the seasons, since every day was divided into twelve equal segments; thus, hours were shorter in winter and longer in summer. Abu'l-Hasan Ibn al-Shatir was aware that "using a gnomon that is parallel to the Earth's axis will produce sundials whose hour lines indicate equal hours on any day of the year." His fragments of his sundial in a Damascus museum is the oldest polar-axis sundial still in existence. The concept later appeared in Western sundials from at least 1446.^[185][186]

Navicula de Venetiis

This was a universal horary dial invented in 9th century Baghdad. It was used for accurate timekeeping by the Sun and Stars, and could be observed from any latitude.^[187] This was later known in Europe as the "Navicula de Venetiis",^[188] which was considered the most sophisticated timekeeping instrument of the Renaissance.^[189]

Compass dial

In the 13th century, Ibn al-Shatir devised a timekeeping device incorporating both a universal sundial and a magnetic compass for the purpose of finding the times of Salah prayers.^[190]

Globes

An armillary sphere.

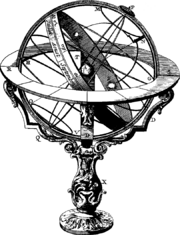
Armillary sphere

An armillary sphere had similar applications to a celestial globe. No early Islamic armillary spheres survive, but several treatises on “the instrument with the rings” were written.

The spherical astrolabe was invented by Islamic astronomers.

Spherical astrolabe

The spherical astrolabe was first produced in the Islamic world.^[191] It was an Islamic variation of the astrolabe and the armillary sphere, of which only one complete instrument, from the 14th century, has survived.

Celestial globes

Celestial globes were used primarily for solving problems in celestial astronomy. Today, 126 such instruments remain worldwide, the oldest from the 11th century. The altitude of the sun, or the Right Ascension and Declination of stars could be calculated with these by inputting the location of the observer on the meridian ring of the globe.

In the 12th century, Jabir ibn Aflah (Geber) was "the first to design a portable celestial sphere to measure and explain the movements of celestial objects."

Seamless celestial globe

The seamless celestial globe invented by Muslim metallurgists and instrument-makers in Mughal India, specifically Lahore and Kashmir, is considered to be one of the most remarkable feats in metallurgy and engineering. All globes before and after this were seamed, and in the 20th century, it was believed by metallurgists to be technically impossible to create a metal globe without any seams. It was in the 1980s, however, that Emilie Savage-Smith discovered several celestial globes without any seams in Lahore and Kashmir. The earliest was invented in Kashmir by the Muslim metallurgist Ali Kashmiri ibn Luqman in 998 AH (1589-90 CE) during Akbar the Great's reign; another was produced in 1070 AH (1659-60 CE) by the Sindhi Astronomer Muhammad Salih Tahtawi with Arabic and Persian inscriptions during the reign of Shah Jahan. 21 such globes were produced, and these remain the only examples of seamless metal globes. These Mughal metallurgists developed the method of lost-wax casting in order to produce these globes.^[192]

These seamless celestial globes are considered to be an unsurpassed feat in metallurgy, hence some consider this achievement to be comparable to that of the Great Pyramid of Giza which was considered an unsurpassed feat in architecture until the 19th century.

Optical instruments

Observation tube

The first reference to an "observation tube" is found in the work of al-Battani (Albatenius) (853-929), and the first exact description of the observation tube was given by al-Biruni (973-1048), in a section of his work that is "dedicated to verifying the presence of the new crescent on the horizon." Though these early observation tubes did not have lenses, they "enabled an observer to focus on a part of the sky by eliminating light interference." These observation tubes were later adopted in Latin-speaking Europe, where they influenced the development of the telescope.^[193]

Experimental device with apertures

In order to prove that "light is emitted from every point of the moon's illuminated surface," Ibn al-Haytham (Alhazen) built an "ingenious experimental device" showing "that the intensity of the light-spot formed by the projection of the moonlight through two small apertures onto a screen diminishes constantly as one of the apertures is gradually blocked up."^[56]

Magnifying lens

The first optical research to describe a magnifying lens used in an instrument was found in a book called the Book of Optics (1021) written by Ibn al-Haytham (Alhazen).^[194] His descriptions were fundamental to the development of the telescope and helped set the parameters in Europe for the later advances in telescopic technology.^[195] His additional work in light refraction, parabolic mirrors, as well as the creation of other instruments such as the camera obscura, also helped spark the Scientific Revolution.^[194][196]

Quadrants

A number of mural instruments, including several different quadrants and sextants, were invented by Muslim astronomers and engineers.

The quadrant was invented by Muhammad ibn Mūsā al-Khwārizmī. This illustration was drawn by Tycho Brahe.

Sine quadrant

The sine quadrant, invented by Muhammad ibn Mūsā al-Khwārizmī in 9th century Baghdad, was used for astronomical calculations.^[197] Also known as the "Sinecal Quadrant" (the Arabic term for it is "Rubul Mujayyab"), it was used for solving trigonometric problems and taking astronomical observations. It was developed by al-Khwarizmi in the 9th century and remained prevalent until the 19th century. Its defining feature is a graph paper like grid on one side that is divided into sixty equal intervals on each axis and is also bounded by a 90 degree graduated arc. A cord was attached to the apex of the quadrant with a bead at the end of it to act as a plumb bob. They were also sometimes drawn on the back of astrolabes.^[198]

Horary quadrant

The first horary quadrant for specific latitudes, was invented by Muhammad ibn Mūsā al-Khwārizmī in 9th century Baghdad, center of the development of quadrants.^[197] It was used to determine time (especially the times of prayer) by observations of the Sun or stars.^[199] The horary quadrant could be used to find the time either in equal or unequal (length of the day divided by twelve) hours. Different sets of markings were created for either equal or unequal hours. For measuring the time in equal hours, the horary quadrant could only be used for one specific latitude while a quadrant for unequal hours could be used anywhere based on an approximate formula. One edge of the quadrant had to be aligned with the sun, and once aligned, a bead on the end of a plumbline attached to the centre of the quadrant showed the time of the day.^[198]

Universal horary quadrant (Quadrans Novus)

The universal horary quadrant was an ingenious mathematical device invented by al-Khwarizmi in 9th century Baghdad and which was later known as the "Quadrans Vetus" (Old Quadrant) in medieval Europe from the 13th century. It could be used for any latitude on Earth and at any time of the year to determine the time in hours from the altitude of the Sun. This was the second most widely used astronomical instrument during the Middle Ages after the astrolabe. One of its main purposes in the Islamic world was to determine the times of Salah.^[197]

Ulugh Beg's mural sextant, constructed in Samarkand, Uzbekistan, during the 15th century.

Astrolabic/Almucantar quadrant (Quadrans Vetus)

The astrolabic or almucantar quadrant was invented in the medieval Islamic world, and it employed the use of trigonometry. The term "almucantar" is itself derived from Arabic.^[200] The almucantar quadrant was originally modified from the astrolabe.^[184] It was invented in Egypt in the 11th or 12th century, and was later known in Europe as the "Quadrans Vetus" (New Quadrant).^[201] It was intended as a simplified alternative to the astrolabe serving a specific latitude. According to David King:^[161]

"This was an invention of some consequence, for the astrolabe, fitted with a series of plates for different latitudes, was neither a practical device nor an accurate observational instrument. Also, being made of brass, it was expensive. The almucantar quadrant, on the other hand, could be made of wood and was an extremely practical device with which one could solve all the problems solvable with an astrolabe, for a particular latitude. The back of such a quandrant could carry a trigonometric grid called a sine quadrant for solving all manner of computational problems."

Universal quadrant (Shakkāzīya)

The universal (shakkāzīya) quadrant was used for solving astronomical problems for any latitude. These quadrants had either one or two sets of shakkāzīya grids and were developed in the 14th century in Syria. Some astrolabes are also printed on the back with the universal quadrant like an astrolabe created by Ibn al-Sarrāj.^[198] The Shakkaziya quadrant produced by Jamal al-Din al-Maridini was an analog computer for solving problems of spherical astronomy.^[202] By the time of the Mamluk Sultanate, Muslim astronomers "developed the quadrant to all conceivable limits; it virtually replaced the astrolabe in Syria and Egypt in Mamluk and Ottoman times."^[161]

Sextants

Mural sextant

The first sextant was constructed in Ray, Iran, by Abu-Mahmud al-Khujandi in 994. It was a very large mural sextant that achieved a high level of accuracy for astronomical measurements, which he described his in his treatise, On the obliquity of the ecliptic and the latitudes of the cities.^[203]

Fakhri sextant

In the 15th century, Ulugh Beg constructed the Fakhri sextant, which had a radius of approximately 36 meters. Constructed in Samarkand, Uzbekistan, the arc was finely constructed with a staircase on either side to provide access for the assistants who performed the measurements.

Framed sextant

At the Istanbul observatory of Taqi al-Din between 1577 and 1580, Taqi al-Din invented the mushabbaha bi'l manattiq, a framed sextant with cords for the determination of the equinoxes similar to what Tycho Brahe later used.^[142]

Other instruments

Various other astronomical instruments were also invented in the Islamic world:

• Alhidade: The alhidade was invented in the Islamic world, while the term "alhidade" is itself derived from Arabic.
• Compendium instrument: A compendium was a multi-purpose astronomical instrument, first constructed by the Muslim astronomer Ibn al-Shatir in the 13th century. His compendium featured an alhidade and polar sundial among other things. Al-Wafa'i developed another compendium in the 15th century which he called the "equatorial circle", which also featured a horizontal sundial. These compendia later became popular in Renaissance Europe.^[184]
• Orthogonal and regular grids: Islamic quadrants used for various astronomical and timekeeping purposes from the 10th century introduced orthogonal and regular grids and markings that are identical to modern graph paper.^[204][205]
• Qibla indicators: In 17th century Safavid Persia, two unique brass instruments with Mecca-centred world maps engraved on them were produced primarily for the purpose of finding the Qibla. These instruments were engraved with cartographic grids to make it more convenient to find the direction and distance to Mecca at the centre from anywhere on the Earth, which may be based on cartographic grids dating back to 10th century Baghdad.^[189] One of the two instruments, produced by Muhammad Husayn,^[206] also had a sundial and compass attached to it.^[207]
• Shadow square: The shadow square was an instrument used to determine the linear height of an object, in conjunction with the alidade, for angular observations.^[208] It was invented by Muhammad ibn Mūsā al-Khwārizmī in 9th century Baghdad.^[209]

List of notable treatises

Zij treatises

• Ibrahim al-Fazari (d. 777) and Muhammad al-Fazari (d. 796/806)
  • Az-Zij ‛alā Sinī al-‛Arab (c. 750)
• Yaqūb ibn Tāriq (d. 796)
  • Az-Zij al-Mahlul min as-Sindhind li-Darajat Daraja
• Muhammad ibn Mūsā al-Khwārizmī (Latinized as Algorismi) (c. 780-850)
  • Zij al-Sindhind (c. 830)
• Muhammad ibn Jābir al-Harrānī al-Battānī (Latinized as Albategni) (853-929)
  • Az-Zij as-Sabi
• Abd Al-Rahman Al Sufi (Latinized as Azophi) (903-986)
  • Book of Fixed Stars (c. 964)
• Ibn Yunus (c. 950–1009)
  • Zij al-Kabir al-Hakimi
• Al-Zarqali (Latinized as Arzachel) (1028–1087)
  • Tables of Toledo
• Al-Khazini (fl. 1115–1130)
  • Az-Zij as-Sanjarī (Sinjaric Tables) (1115–1116)
• Nasīr al-Dīn al-Tūsī (1201–1274)
  • Zij-i Ilkhani (Ilkhanic Tables) (1272)
• Jamshīd al-Kāshī (1380–1429)
  • Khaqani Zij
• Ulugh Beg (1394–1449)
  • Zij-i-Sultani (1437)
• Taqi al-Din (1526–1585)
  • Unbored Pearl (1577–1580)

Almanacs

The word "Almanac" is an Arabic word.^[210] The modern almanac differs from earlier astronomical tables (such as the earlier Babylonian, Ptolemaic and Zij tables) in the sense that "the entries found in the almanacs give directly the positions of the celestial bodies and need no further computation", in contrast to the more common "auxiliary astronomical tables" based on Ptolemy's Almagest. The earliest known almanac in this modern sense is the Almanac of Azarqueil written in 1087 by Abū Ishāq Ibrāhīm al-Zarqālī (Latinized as Azarqueil) in Toledo, Al-Andalus. The work provided the true daily positions of the sun, moon and planets for four years from 1088 to 1092, as well as many other related tables. A Latin translation and adaptation of the work appeared as the Tables of Toledo in the 12th century and the Alfonsine tables in the 13th century.^[211]

Treatises on instruments

In the 12th century, al-Khazini wrote the Risala fi'l-alat (Treatise on Instruments) which has seven parts describing different scientific instruments: the triquetrum, dioptra, a "triangular instrument", the quadrant, the astrolabe, and instruments involving reflection.^[212]

In 14th century Egypt, Najm al-Din al-Misri (c. 1325) wrote a treatise describing over 100 different types of scientific and astronomical instruments, many of which he invented himself.^[189]

In 1416, al-Kashi wrote the Treatise on Astronomical Observational Instruments, which described a variety of different instruments, including the triquetrum and armillary sphere, the equinoctial armillary and solsticial armillary of Mo'ayyeduddin Urdi, the sine and versine instrument of Urdi, the sextant of al-Khujandi, the Fakhri sextant at the Samarqand observatory, a double quadrant Azimuth-altitude instrument he invented, and a small armillary sphere incorporating an alhidade which he invented.^[213]

Other works

• Ja'far Muhammad ibn Mūsā ibn Shākir (Latinized as Mohammed Ben Musa) (800-873)
  • Book on the motion of the orbs
  • Astral Motion
  • The Force of Attraction
• Ahmad ibn Muhammad ibn Kathīr al-Farghānī (Latinized as Alfraganus) (d. 850)
  • Elements of astronomy on the celestial motions (c. 833)
  • Kitab fi Jawami Ilm al-Nujum
• Ibn al-Haytham (Latinized as Alhacen) (965-1039)
  • On the Configuration of the World
  • Doubts concerning Ptolemy (c. 1028)
  • The Resolution of Doubts (c. 1029)
  • The Model of the Motions of Each of the Seven Planets (1029–1039)
• Abū Rayhān al-Bīrūnī (973–1048)
  • Kitab al-Qanun al-Mas'udi (Latinized as Canon Mas’udicus) (1031)
• Abu Ubayd al-Juzjani (c. 1070)
  • Tarik al-Aflak (1070)
• Al-Istidrak ala Batlamyus (Recapitulation regarding Ptolemy) (11th century)
• Al-Khazini (fl. 1115–1130)
  • Risala fi'l-alat (Treatise on Instruments)
• Nasīr al-Dīn al-Tūsī (1201–1274)
  • Al-Tadhkirah fi'ilm al-hay'ah (Memento in astronomy)
• Najm al-Dīn al-Qazwīnī al-Kātibī (d. 1277)
  • Hikmat al-'Ain
• Qutb al-Din al-Shirazi (1236–1311)
  • The Limit of Accomplishment concerning Knowledge of the Heavens
• Ibn al-Shatir (1304–1375)
  • A Final Inquiry Concerning the Rectification of Planetary Theory
• Ali al-Qushji (d. 1474)
  • Concerning the Supposed Dependence of Astronomy upon Philosophy
• Shams al-Din al-Khafri (d. 1525)
  • The complement to the explanation of the memento

Arabic star names

Many of the modern names for numerous stars and constellations are derived from their Arabic language names. Examples include: Acamar, Aldebaran, Algol, Altair, Baham, Baten Kaitos, Caph, Dabih, Edasich, Furud, Gienah, Hadar, Izar, Jabbah, Keid, Lesath, Mirak, Nashira, Okda, Phad, Rigel, Sadr, Tarf, and Vega, as well as a number of other stars. Some of these names originated in the pre-Islamic Arabian Peninsula, but many came later, some as translations of ancient Greek descriptions and others of unknown origin.^[214]

Notes

See also

• Arab and Persian astrology
• Hebrew astronomy
• History of astronomy
• Inventions in the Muslim world
• Islamic astrology
• Islamic Golden Age
• List of Arabic star names
• List of Arab scientists and scholars
• List of Iranian scientists and scholars
• List of Muslim astronomers
• List of Muslim scientists
• Physics in medieval Islam
• Science in medieval Islam
• Sufi cosmology
• Zij

References

External links

• "How Greek Science Passed to the Arabs" by De Lacy O'Leary
• The Arab Union for Astronomy and Space Sciences (AUASS)
• King Abdul Aziz Observatory
• History of Islamic Astrolabes

Islamic studies Arts Architecture • Calligraphy • Literature • Music • Poetry • Pottery • Influences on Christian Art Economics Economic History • Agency • Banking • Capitalism • Poverty • Socialism • Trust • Usury • Welfare History Timeline • Historiography • Social Changes • Conquests • Golden Age • Agricultural Revolution • Economic History • Contributions to Medieval Europe • European Renaissance Law & Politics Anarchism • Democracy (Consensus • Consultation) • Feminism • Jurisprudence (Analogy • Ijtihad • Madh'hab) • Peace • Quietism • Secularism • Social Changes • State Philosophy Early Philosophy • Contemporary Philosophy • Theology (Kalam) • Ethics • Logic • Metaphysics • Astrology • Sociology (Medieval Sociology • Asabiyyah) Science & Technology Timeline • Agriculture • Alchemy & Chemistry • Astronomy (Cosmology) • Geography & Cartography • Inventions • Mathematics • Medicine (Ophthalmology) • Physics • Psychology Other fields Education (Ijazah • Maktab) • Sufi Studies (Mysticism • Cosmology • Philosophy)